Review Request: Generating boolean expression from "list of switches"
Hi,
This is less a question than a review request for more veteran MPS users, but maybe it is also interesting for others.
Imagine a language where users can declare Switches like so:
foo is on
bar is off
baz is off
Furthermore, Conditions can be declared like so:
set FooBar when foo is on
bar is on
set BarNoBaz when bar is on
baz is off
Switches can be flipped later in the language, but that's of no concern for now.
The idea is to "abstract away" the 'AND', 'OR', and 'NOT' operators and still allow users to have a basic set of boolean logic.
Now, you want to generate a Java InstanceMethodDeclaration for each Condition, e.g.:
With 'bar' and 'baz' being boolean fields generated for the Switches.
My way of doing this seems rather heavy handed, so I was hoping for some feedback on where I could improve.
Here's the structure for the relevant concepts:
SwitchRefWithTarget allows to define a target value for a switch that must apply for the condition to be true. SwitchState is an enum with on/off as members and Switch is a INamedConcept.
For each of these concepts, there is one reduction rule defined:
Condition (this one is pretty strait forward, I guess):
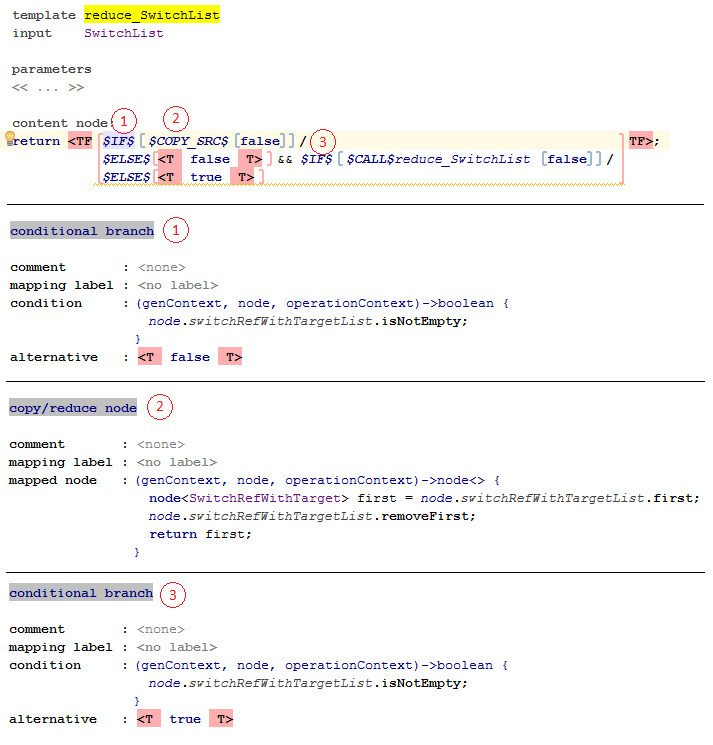
SwitchList:
Here, we first check if there are any entries in the list of references and default to false if not (first base case of recursion). Otherwise (point 2), we take the first element, a SwitchRefWithTarget, and put its output there (see below). We also remove it from the list to make sure it will only be reduced once. That way, we generated the first LeftExpression of our AndExpression.
For the RightExpression, we either call the template again, now without the first element in the list, or we create a "dangling right expression" which is just the constant true. The second base case to end the recursion.
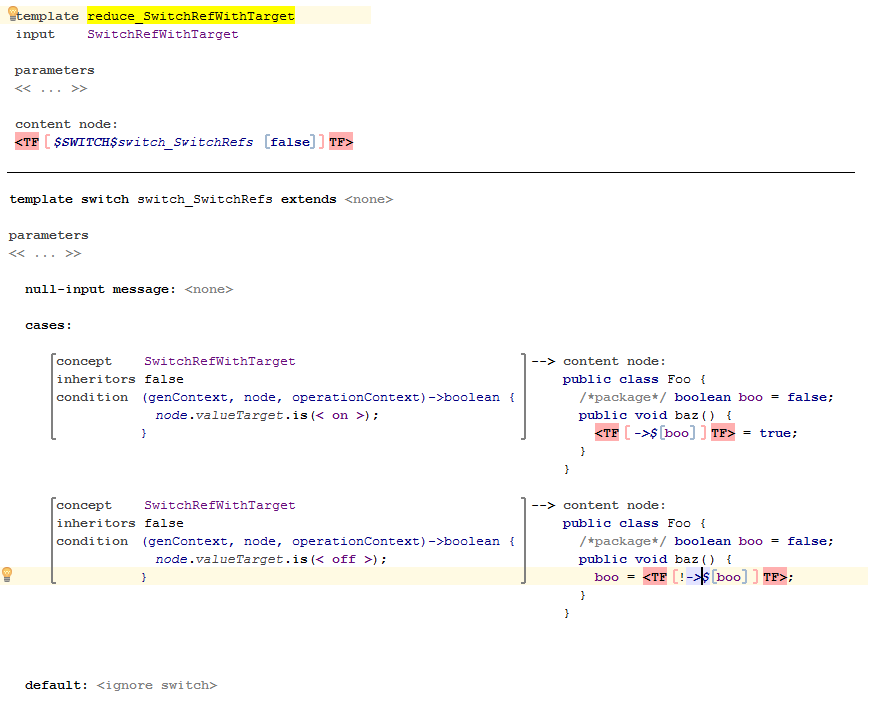
SwitchRefWithTarget:
To deal with the "NOT" operator, this template uses a SWITCH. For generating the reference to the boolean variable, I make use of a label mapping.
Finally, I remove all "dangling ANDs" via a post-processing script:
Let me know if I could have taken significant short-cuts or if this approach is bad for whatever reason.
Thanks,
Robert
This is less a question than a review request for more veteran MPS users, but maybe it is also interesting for others.
Imagine a language where users can declare Switches like so:
foo is on
bar is off
baz is off
Furthermore, Conditions can be declared like so:
set FooBar when foo is on
bar is on
set BarNoBaz when bar is on
baz is off
Switches can be flipped later in the language, but that's of no concern for now.
The idea is to "abstract away" the 'AND', 'OR', and 'NOT' operators and still allow users to have a basic set of boolean logic.
Now, you want to generate a Java InstanceMethodDeclaration for each Condition, e.g.:
private boolean BarNoBaz() {
return bar && !baz;
}
With 'bar' and 'baz' being boolean fields generated for the Switches.
My way of doing this seems rather heavy handed, so I was hoping for some feedback on where I could improve.
Here's the structure for the relevant concepts:
concept Condition extends BaseConcept implements INamedConcept instance can be root: false alias: <no alias> short description: <no short description> properties: << ... >> children: switchList : SwitchList[1] references: << ... >>
concept SwitchList extends BaseConcept implements <none> instance can be root: false alias: <no alias> short description: <no short description> properties: << ... >> children: switchRefWithTarget: SwitchRefWithTarget[1..n] references: << ... >>
SwitchRefWithTarget allows to define a target value for a switch that must apply for the condition to be true. SwitchState is an enum with on/off as members and Switch is a INamedConcept.
concept SwitchRefWithTarget extends BaseConcept implements <none> instance can be root: false alias: <no alias> short description: <no short description> properties: valueTarget : SwitchState children: << ... >> references: ref : Switch[1]
For each of these concepts, there is one reduction rule defined:
Condition (this one is pretty strait forward, I guess):
SwitchList:
Here, we first check if there are any entries in the list of references and default to false if not (first base case of recursion). Otherwise (point 2), we take the first element, a SwitchRefWithTarget, and put its output there (see below). We also remove it from the list to make sure it will only be reduced once. That way, we generated the first LeftExpression of our AndExpression.
For the RightExpression, we either call the template again, now without the first element in the list, or we create a "dangling right expression" which is just the constant true. The second base case to end the recursion.
SwitchRefWithTarget:
To deal with the "NOT" operator, this template uses a SWITCH. For generating the reference to the boolean variable, I make use of a label mapping.
Finally, I remove all "dangling ANDs" via a post-processing script:
mapping script RemoveDanglingAnd
script kind : post-process output model
(genContext, model, operationContext)->void {
foreach it in model.nodes(AndExpression) {
if (it.rightExpression.isInstanceOf(BooleanConstant) && it.rightExpression : BooleanConstant.value == true) {
it.replace with(it.leftExpression);
}
}
}
Let me know if I could have taken significant short-cuts or if this approach is bad for whatever reason.
Thanks,
Robert
Please sign in to leave a comment.


the only suggestion I have, although I might be missing some points, is to replace the recursion with the LOOP macro iterating over node.switchRefTargetWithTargetList inside reduce_SwitchList, perhaps wrapped in an IF, so as "false" is generated for empty collection. You will be able to remove the post-processing script then, as well.
Vaclav
Thanks for your feedback.
I do not see how one can utilize a LOOP macro to create an AndExpression with an unknown number of AndExpression children.
For a switchList of two items {a, b}, I want to create a tree like so:
&&
|_a
|_b
For a list of three items {a, b, c}, the tree look like this:
&&
|_a
|_&&
|_b
|_c
and so forth.